Definition des Differenzwerts (Dreiecksymbol + Variable)

[freddy123]

Ich wollte von euch wissen, ob ich das Bild hier als Definition des "Differenzwerts" ansehen kann (siehe Anhang), ansonsten seh ich auf jeder Seite meines Physikbuchs nur blue screen.

 

[SchwarzeBeere]

Das kommt ganz auf dein Physikbuch, die darin enthaltene Definition und den Kontext drauf an. Um was geht es denn genau?

(Formeln kannst du auch übrigens hier schöner schreiben, um sie im Forum zu posten, so z.B.

).

 

[freddy123]

Ob man den Differenzwert einer Größe (mit dem Dreieck davor) unmissverständlich definieren kann als Differenzwert einer Größe zu welcher anderen?

 

[SchwarzeBeere]

Entweder steht das in deinem Buch, oder es ergibt sich aus den Formeln, die

enthalten.

Folgende Lösungen sind z.B. möglich:
-

-

-

-

- usw..

Normalerweise gilt:

. Einfach so mal hier ein

, da ein

, ohne die Funktion zu definieren (

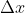bedeutet nichts anderes als

) oder eine Definition vorauszusetzen ist weder schön, noch üblich. Deswegen auch die Frage, wo dein konkretes Problem ist und welche Formel das

enthält. Eventuell kann man daraus - wenns in einem Buch steht, wird es ja wohl bekannt sein - die Bedeutung ableiten und dir so helfen.

 

[freddy123]

Die Bruchdehnung eines Werkstoffs A = /\lu / l0 = (lu - l0) / l0

Die Brucheinschnürung Z = (S0 - Su) / S0

l0 ist die Anfangslänge vor der Beanspruchung der Probe auf Zug, zumindest aus dem Sinnzusammenhang lässt sich also erschließen, dass bei lu für die Länge des Probestabs bei Bruch /\lu = lu - l0 = Verlängerung beim Bruch

S0 steht für die Querschnittsfläche der Probe vor dem Zug und Su für die Querschnittsfläche an der Bruchstelle. Kann ich die Formel Z = (S0 - Su) / S0 auf Z = /\S0 / S0 vereinfachen?

Ob ich mir aufgrund des Sinnzusammenhangs vom folgenden Code die zweite Zeile sparen kann:

    Z = /\S0 / S0
^  /\S0 = S0 - Su

Das Buch macht mir eigentlich keine Probleme, ich will in einer Klassenarbeit lediglich nicht mit falscher Namensgebung der Formelzeichen auf das richtige Ergebnis kommen.

 

[benediktibk]

Wenn die Definition in der Form einmal vorkommt, entweder in der Angabe oder in deiner Antwort, dann kannst du Sie dir ab dem Punkt ersparen. Sollte die Notation wirklich sehr gängig sein in dem Fach musst du es vermutlich gar nicht definieren, dann kann man davon ausgehen dass der Lehrer schon weiß das du meinst. Im Zweifelsfall würde ich aber den Lehrer einfach fragen, der beißt sicher nicht.

mfg benediktibk

 

[freddy123]

Im Zweifelsfall würde ich aber den Lehrer einfach fragen, der beißt sicher nicht.

mfg benediktibk

Das ist ja das Problem, der beißt, und man kann ihn auch nichts fragen.

Ich definier's einfach in jedem Rechenweg neu.