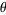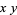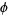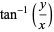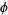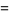[C++] Zwei Winkel in Vektor umwandeln (und zurück)

[bad_alloc]

Hi HaBo,
ich versuche gerade den Normalenvektor der Bildebene der Kamera von Irrlicht zu bestimmen. Die Kamerarotation wird in zwei Winkeln zurückgeliefert: Die Rotation um die X-Achse (Phi) und die Rotation um die Y-Achse (Theta). Aus diesen Winkeln möchte ich einen Vektor bestimmen und diesen später dann auch wieder in die Winkel zurück umrechnen. Im Grunde ist es also eine Umwandlung von karthesischen Koordinaten zu sphärischen Koordinaten. Ich verwende dazu folgenden Code:

vectorObj convertAnglesToVector(anglePair angles) {
    vectorObj result;
    double rPhi   = (angles.phi   * pi) / 180;
    double rTheta = (angles.theta * pi) / 180;

    result.X = cos(rPhi) * sin(rTheta);
    result.Y = sin(rPhi) * sin(rTheta);
    result.Z = cos(rTheta);

    return result;
}

anglePair convertVectorToAngles(vectorObj vector) {
    double x = vector.X;
    double y = vector.Y;
    double z = vector.Z;

    anglePair result;

    if (sqrt(x*x + y*y + z*z) != 0.0) {
        result.theta = (acos(z) * (180 / pi));
        result.phi   = (atan2(y, x) * (180 / pi));
    } else {
        result.theta = result.phi = 0.0;
    }
    return result;
}

Die Formeln habe ich von Wolfram Math World übernommen. Irrlicht hat jetzt jedoch ein anderes Koordinatensystem als Wolfram:

Die Rotationen werden im Bereich von 0° bis 360° angegeben, wie eingezeichnet. Nun versagt die Umwandlung von einen Vektor in ein Gradzahlenpaar, wenn der Vektor im Bereich 180 < Thetha < 360 ist. Wo liegt mein Fehler? Die Formeln sind eins zu eins übernommen. Kann es sein, dass ich für die Winkelfunktionen Bogenmaßwerte benötige? Sind meine Winkel anders als die von Wolfram?


Ohne korrekte Rotation,

bad_alloc

 

[sTEk]

Also, nur zum Verständnis Deiner Irrlicht-Anwendung:

• Phi ist der Drehwinkel der "x-Achse"
• Theta ist der Drehwinkel der "y-Achse"
• der Radius-Vektor r ist in deinem Fall v

Somit hast Du natürlich völlig richtig die Winkel aus den Angaben von Wolfram vertauscht. (Zitat: "... with

remaining the angle in the

-plane and

becoming the angle out of that plane. ")


Du musst die Winkel natürlich auch - wie Du schon machst - ins Bogenmaß umrechnen. (Zitat: "... where

,

, and

...")


In Deinem Fall bedeutet das allerdings:

• φ Є [0, 2π]
• θ Є [0, π]

Wie Du siehst, muss die Rechnung für

wenn der Vektor im Bereich 180 < Thetha < 360 ist.

versagen.


Du benötigst die Konvention θ Є [-π/2, π/2]!


Als erstes musst Du also sicher stellen, dass die Winkel 90 < θ ≤ 180° auf den Bereich 0 < θ ≤ 90° und 180 < θ ≤ 270° auf den Bereich 0 > θ ≥ -90° gewandelt werden!

Die C++-Funktion atan2 behandelt x und y bereits so, wie es die atan2-Funktion vorschreibt.

Theta berechnet sich dann jedoch anders, es folgen also diese Rechnungen:

• θ = arcsin(z) | [r=1]
• φ = atan2(y, x) | [r=1]

Bei der Transformation von polaren in kartesische Koordinaten ergibt sich dann für Dich folgendes:

• x = cos(θ) * cos(φ)
• y = sin(θ) * cos(φ)
• z = sin(φ)

 

[Tsjuder]

Als ich vor Ewigkeiten mal mit OpenGL gearbeitet habe, kann ich mich noch an ähnliche Probleme erinnern.

Ich hab sowieso gerade noch ein paar Verständniss Probleme:
Wieso kannst du bei "convertAnglesToVector" bei result.* immer das "r*" weglassen? Laut Wikipedia gilt z.B. result.x = r * sin(theta) * cos(phi).

Die Koordinaten sollten immer im Bogenmaß angegeben werden.

Sollte "result.theta = (acos(z) * (180 / pi));" nicht mit acos(z/r) berechnet werden oder wieso lässt du den Divisor weg?

Desweiteren gilt übrigens laut Wikipedia, dass der Winkel Theta, derjenige Winkel zwischen der z-Achse und r ist und dieser auch nur von 0 bis Pi, also 0° bis 180°, gezählt wird. Demnach wäre 180 < Thetha < 360 gar nicht möglich.

Schau am Besten selbst nochmal rein: Kugelkoordinaten
Ansonsten wäre zumindestens mir ein lauffähiges Beispiel, wo es klappt und wo nicht hilfreich.

Vielleicht hat es dir geholfen, aber wie gesagt: Bei mir ist das schon echt lange her und so "trocken" fällt mir Geometrie immer schwer


EDIT: Während ich das Fenster auf hatte, hat sTEk gepostet und die Antwort ist sowieso wesentlich qualifizierter, daher ist alles durchgestrichen.

 

[bad_alloc]

Vielen vielen Dank an sTek für diese sehr anschauliche Antwort :thumb_up:
Ebensoviel Dank an Tsjuder für die synchrone Hife.

EDIT: Ich hab mich zu früh gefreut. In sTeks Zeichnung ist Phi die Rotation um die Z-Achse, wenn man die Irrlicht "Logik" anwendet. Theta ist die Rotation um die korrekte (X) Achse, allerdings ist die Rotationsrichtung umgekeht. Wie muss man die Formeln nun ändern?

 

[sTEk]

Also, im Endeffekt ist es doch alles eine Frage der Definitionen. Wenn phi flach auf dem Boden liegt und somit die Rotation der Z-Achse beschreibt, dann muss man lediglich die Formeln umschreiben und aus y ein z machen und umgekehrt, schließlich sollte das Kommutativgesetz greifen.

Ohne es überprüft zu haben:

• θ = arcsin | [r=1]
• φ = atan2(z, x) | [r=1]

• x = cos(θ) * cos(φ)
• z = sin(θ) * cos(φ)
• y = sin(φ)