Guten Morgen zusammen...
gegeben sei folgende formale Grammatik G = (N, T, P, s) , mit
N = {GZAHL, ZIFFER, GZ, ZAHL}
T = {0,1,2,3,4,5,6,7,8,9}
P = {GZAHL -> GZ | ZAHL GZ,
ZAHL -> ZIFFER | ZIFFER ZAHL,
Ziffer -> 0 | 1 | 2 | 3 | 4 | 5 | 6 |7 | 8 | 9 | ,
GZ -> 0 | 2 | 4 | 6 | 8 }
s= GZAHL.
Ich frage mich, von welchem Typ diese Grammatik ist (Typ2 ?)
Die eigentliche Frage ist aber:
Auf einem Blatt zur theoretischen Informatik, welches wir erhalten haben sind Typ3 Grammatiken definiert als
das verstehe ich so, dass auf der linken Seite genau ein Nichtterminal stehen muss, auf der rechten Seite beliebig viele Terminale (wegen T*). oder aber beliebig viele Terminale und ein NIchtterminal.
Diese Definition widerspricht sich aber entweder mit anderen Definitionen, die ich gefunden habe, oder ich habe die Definition oben falsch gedeutet (bin noch nicht sonderlich geübt in dieser Schreibweise)
Beispielsweise finde ich auf einer anderen Seite:
also auf der rechten Seite entweder genau ein Terminal oder ein Terminal und ein NIchtterminal....
Ist die Blattdefinition einfach fehlerhaft ?
gegeben sei folgende formale Grammatik G = (N, T, P, s) , mit
N = {GZAHL, ZIFFER, GZ, ZAHL}
T = {0,1,2,3,4,5,6,7,8,9}
P = {GZAHL -> GZ | ZAHL GZ,
ZAHL -> ZIFFER | ZIFFER ZAHL,
Ziffer -> 0 | 1 | 2 | 3 | 4 | 5 | 6 |7 | 8 | 9 | ,
GZ -> 0 | 2 | 4 | 6 | 8 }
s= GZAHL.
Ich frage mich, von welchem Typ diese Grammatik ist (Typ2 ?)
Die eigentliche Frage ist aber:
Auf einem Blatt zur theoretischen Informatik, welches wir erhalten haben sind Typ3 Grammatiken definiert als
" vom Typ 3 oder regulär, wenn gegenüber Typ 2 für jede Regel einschränkend X -> y oder X -> yYgilt, wobei y € T*, X,Y € N "
das verstehe ich so, dass auf der linken Seite genau ein Nichtterminal stehen muss, auf der rechten Seite beliebig viele Terminale (wegen T*). oder aber beliebig viele Terminale und ein NIchtterminal.
Diese Definition widerspricht sich aber entweder mit anderen Definitionen, die ich gefunden habe, oder ich habe die Definition oben falsch gedeutet (bin noch nicht sonderlich geübt in dieser Schreibweise)
Beispielsweise finde ich auf einer anderen Seite:
Typ 3regulär Die Regeln im Regelsystem müssen die folgende Form haben
wobei A Nonterminal und a Terminal ist.
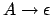
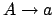
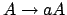
also auf der rechten Seite entweder genau ein Terminal oder ein Terminal und ein NIchtterminal....
Ist die Blattdefinition einfach fehlerhaft ?